1. 1. 数据结构概述
    1. 1.1. 1.数据结构的基本概念
      1. 1.1.1. 1.1.数据的逻辑结构
      2. 1.1.2. 1.2.数据的存储结构
      3. 1.1.3. 1.3.数据的运算
      4. 1.1.4. 1.4.数据结构与数据类型
    2. 1.2. 2.算法的基本概念
      1. 1.2.1. 2.1.算法及其特征
      2. 1.2.2. 2.2.算法描述
      3. 1.2.3. 2.3.算法分析
        1. 1.2.3.1. 2.3.1.时间复杂度
        2. 1.2.3.2. 2.3.2.空间复杂度
  2. 2. 线性表
    1. 2.1. 1.线性表的基本概念
      1. 2.1.1. 1.1.线性表的定义
      2. 2.1.2. 1.2.线性表的特征
      3. 2.1.3. 1.3.线性表的基本运算
    2. 2.2. 2.线性表的存储结构
      1. 2.2.1. 2.1.顺序存储结构
      2. 2.2.2. 2.2.链式存储结构
    3. 2.3. 3.顺序表的基本运算
      1. 2.3.1. 3.1.线性表的定义
      2. 2.3.2. 3.2.初始化线性表
      3. 2.3.3. 3.3.求线性表长度
      4. 2.3.4. 3.4.求线性表中第i个元素
      5. 2.3.5. 3.5.按值查找
      6. 2.3.6. 3.6.插入元素
      7. 2.3.7. 3.7.删除元素
      8. 2.3.8. 3.8.输出线性表
      9. 2.3.9. 3.9.main
    4. 2.4. 4.单链表的基本运算
      1. 2.4.1. 4.1.单链表的定义
      2. 2.4.2. 4.2.初始化单链表
      3. 2.4.3. 4.3.求线性表的长度
      4. 2.4.4. 4.4.求线性表中第i个元素
      5. 2.4.5. 4.5.按值查找
      6. 2.4.6. 4.6.插入结点
      7. 2.4.7. 4.7.删除结点
      8. 2.4.8. 4.8.输出单链表
      9. 2.4.9. 4.9.main
    5. 2.5. 5.链表的基本运算(By-Go)
    6. 2.6. 6.循环单链表的基本运算
      1. 2.6.1. 6.1.循环单链表的定义
      2. 2.6.2. 6.2.初始化循环单链表
      3. 2.6.3. 6.3.求线性表的长度
      4. 2.6.4. 6.4.求线性表中第i个元素
      5. 2.6.5. 6.5.按值查找
      6. 2.6.6. 6.6.插入结点
      7. 2.6.7. 6.7.删除结点
      8. 2.6.8. 6.8.输出线性表
      9. 2.6.9. 6.9.main
    7. 2.7. 7.双链表的基本运算
      1. 2.7.1. 7.1.双链表的定义
      2. 2.7.2. 7.2.初始化双链表
      3. 2.7.3. 7.3.求表长运算
      4. 2.7.4. 7.4.求线性表中第i个元素
      5. 2.7.5. 7.5.按值查找
      6. 2.7.6. 7.6.插入运算
      7. 2.7.7. 7.7.删除运算
      8. 2.7.8. 7.8.输出线性表
      9. 2.7.9. 7.9.main
    8. 2.8. 8.循环双链表的基本运算
      1. 2.8.1. 8.1.循环双链表的定义
      2. 2.8.2. 8.2.初始化循环双链表
      3. 2.8.3. 8.3.求表长运算
      4. 2.8.4. 8.4.求线性表中第i个元素
      5. 2.8.5. 8.5.按值查找
      6. 2.8.6. 8.6.插入运算
      7. 2.8.7. 8.7.删除运算
      8. 2.8.8. 8.8.输出线性表
      9. 2.8.9. 8.9.main
    9. 2.9. 9.顺序表求约瑟夫问题
    10. 2.10. 10.两个多项式相加运算
  3. 3. 栈
    1. 3.1. 1.栈的基本概念
      1. 3.1.1. 1.1.栈的定义
      2. 3.1.2. 1.2.栈的特征
      3. 3.1.3. 1.3.栈的基本运算
    2. 3.2. 2.栈的存储结构
      1. 3.2.1. 2.1.顺序存储结构
      2. 3.2.2. 2.2.链式存储结构
    3. 3.3. 3.顺序栈基本运算
      1. 3.3.1. 3.1.栈的定义
      2. 3.3.2. 3.2.初始化栈
      3. 3.3.3. 3.3.进栈运算
      4. 3.3.4. 3.4.出栈运算
      5. 3.3.5. 3.5.取栈顶元素
      6. 3.3.6. 3.6.判断栈空运算
      7. 3.3.7. 3.7.main
    4. 3.4. 4.链栈基本运算
      1. 3.4.1. 4.1.链式栈的定义
      2. 3.4.2. 4.2.初始化栈
      3. 3.4.3. 4.3.进栈运算
      4. 3.4.4. 4.4.出栈运算
      5. 3.4.5. 4.5.取栈顶元素运算
      6. 3.4.6. 4.6.判断栈空运算
      7. 3.4.7. 4.7.main
    5. 3.5. 5.栈的基本运算(By-Go)

数据结构笔记归档1

数据结构概述

1.数据结构的基本概念

数据结构是研究各种数据的特性以及数据之间存在的关系，进而根据实际应用的要求，合理地组织和存储数据，设计出相应的算法。

数据是对客观事物的符号表示。

  • 数据元素（节点）：数据的基本单位，在程序中通常作为一个整体进行考虑和处理。一个数据元素可以由若干个数据项组成。
  • 数据项：具有独立含义的最小标识单位。例如，一条数据记录可以称为一个数据元素，数据记录的某个字段就是一个数据项。
  • 数据结构：相互之间存在一种或多种特点关系的数据元素的集合。

1.1.数据的逻辑结构

数据的逻辑结构：数据元素与数据元素之间的逻辑关系。可以分为四类基本结构：

  • 集合：结构中的数据元素属于一个集合（集合类型元素之间过于松散）
  • 线性结构：结构中的数据元素存在一对一的关系
  • 树形结构：结构中的数据元素存在一对多的关系
  • 图形结构：结构中的数据元素存在多对多的关系

数据的逻辑结构可以用以下的二元组来表示：

1
S=(D,R)

其中，D是数据节点的有限集合，R是D上的关系的有限集合，其中每个关系都是从D到D的关系。

例如：

1
2
3
4
S = (D,R)
D = {1,2,3,4}
R = {r}
r = {<1,2>,<1,3>,<3,4>}

说明：

  • 尖括号表示有向关系，例如<a,b>，表示a→b
  • 圆括号表示无向关系，例如(a,b)，表示a→b,b→a
  • 前驱结点：中a是b的前驱结点
  • 后继结点：中b是a的后继结点
  • 开始结点：没有前驱结点
  • 终端结点：没有后继结点
  • 内部结点：既有前驱结点，又有后继结点

1.2.数据的存储结构

数据在计算机中的存储表示称为数据的存储结构，又称物理结构。 数据存储到计算机中即要求存储各节点的数值，又要存储结点与结点之间的逻辑关系。 以下介绍四种基本的存储结构：顺序存储、链式存储、索引存储、散列存储。

1.顺序存储结构

顺序存储结构是把逻辑上相邻的元素存储在一组连续的存储单元中，其元素之间的逻辑关系由存储单元地址间的关系隐含表示。

优点：节省存储空间，只需要存储数据结点，并不需要存储结点的逻辑关系。 缺点：不便于修改，插入和删除某个结点需要修改一系列的结点。

2.链式存储结构

链式存储结构，给每个结点增加指针字段，用于存放临近结点的存储地址，每个结点占用两个连续的存储单元，一个存放数据，一个存放临近结点（前驱/后继结点）的地址。

优点：便于修改，修改时只需要修改结点的指针字段，不需要移动其他结点。 缺点：占用存储空间，因为需要存储结点之间的逻辑关系。因为结点之间不一定相邻，因此不能对结点进行随机访问。

3.索引存储结构

索引存储结构即在存储结点的同时，增加索引表，索引表的索引项为：（关键字，地址），关键字标识结点，地址为结点的指针。各结点的地址在索引表中是依次排列的。

优点：可以快速查找，可以随机访问，方便修改。 缺点：建立索引表增加了时间和空间的开销。

4.散列存储结构

散列存储结构是根据结点的值确定结点的存储地址。以结点作为自变量，通过散列函数算出结果i，再把i作为结点的存储地址。

优点：查找速度快，适用于快速查找和插入的场景。 缺点：只存结点数据，不存结点之间的关系。

1.3.数据的运算

数据的运算就是施加于数据的操作，例如对一张表进行增删改查操作，一般数据结构中的运算除了加减乘除外还会涉及算法问题。

1.4.数据结构与数据类型

按某种逻辑关系组成的数据元素，按一定的存储方式存储于计算机中，并在其上定义了一个运算的集合，称为一个数据结构。

1
数据结构 = 数据的逻辑结构 + 数据的存储结构 + 数据的运算(算法)

数据类型是程序设计语言中对数据结构的实现，数据类型明显或隐含地规定了数据的取值范围、存储方式及允许进行的运算。

常用的数据类型：

  1. 基本数据类型
  2. 指针类型
  3. 数组类型
  4. 结构体类型
  5. 组合体类型
  6. 自定义类型

2.算法的基本概念

2.1.算法及其特征

算法是对特定问题求解步骤的描述，是指令的有限序列，每条指令包含一个或多个操作。

特点：

  • 有穷性：有限的步骤和有限的时间内完成
  • 确定性：每个指令有确定的含义
  • 可行性：算法是可以实现的
  • 输入性：一个或多个输入
  • 输出性：一个或多个输出

2.2.算法描述

  1. 输入语句
  2. 输出语句
  3. 赋值语句
  4. 条件语句
  5. 循环语句
  6. 返回语句（return）
  7. 定义函数语句
  8. 调用函数语句

2.3.算法分析

2.3.1.时间复杂度

算法分析主要涉及时间复杂度和空间复杂度。一般情况我们讨论时间复杂度。

  • 频度：某语句在算法中被执行的次数。
  • T(n)：所有语句的频度之和，n为问题规模。
  • 时间复杂度：当n趋于无穷大时，T(n)的数量级。记作T(n)=O(f(n)), O的含义是T(n)的数量级。

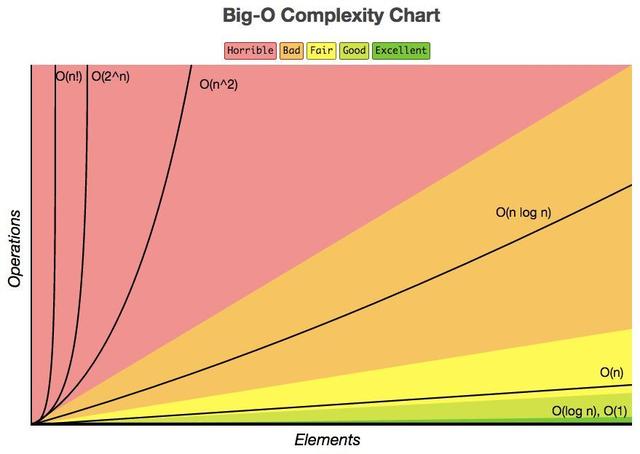
用数量级O(f(n))表示算法执行时间T(n)时，f(n)一般去简单形式：1，log2n，n，nlog2n，n2，n3，2n。

时间复杂度的关系如下：

O(1) < O(log2n) < O(n) < O(nlog2n) < O(n2) < O(n3) < O(2n)

时间复杂度函数对比:

2.3.2.空间复杂度

一个算法的空间复杂度是指该算法所耗费的存储空间，计算公式计作：S(n) = O(f(n))。其中 n 也为数据的规模，f(n) 在这里指的是 n 所占存储空间的函数。

常用的空间复杂度：

  • 空间复杂度 O(1)
  • 空间复杂度 O(n)
  • 空间复杂度 O(n2)

线性表

1.线性表的基本概念

线性表是最基本、最简单、也是最常用的一种数据结构。线性表（linear list）是数据结构的一种，一个线性表是n个具有相同特性的数据元素的有限序列。

线性表中数据元素之间的关系是一对一的关系，即除了第一个和最后一个数据元素之外，其它数据元素都是首尾相接的（注意，这句话只适用大部分线性表，而不是全部。比如，循环链表逻辑层次上也是一种线性表（存储层次上属于链式存储，但是把最后一个数据元素的尾指针指向了首位结点）。

1.1.线性表的定义

线性表是由n（n>=0）个结点组成的有限序列，通常表示成（a1,a2,…,an），满足以下特征。

1.2.线性表的特征

  • 线性表中每个结点至多只有一个前驱结点且至多只有一个后继结点
  • 起始结点没有前驱结点
  • 终结结点没有后继结点

1.3.线性表的基本运算

  • 初始化线性表
  • 求线性表的长度
  • 求线性表的第i个元素
  • 按值查找元素，返回元素序号
  • 插入元素
  • 删除元素
  • 输出列表

2.线性表的存储结构

2.1.顺序存储结构

1
2
3
4
5
6
7
8
9
#define MAXSIZE 100 /*顺序表的容量*/

typedef char ElemType;

typedef struct
{
    ElemType data[MAXSIZE]; /*存放顺序表的元素*/
    int length;                /*顺序表的实际长度*/
} SqList;

2.2.链式存储结构

单链表

1
2
3
4
5
6
7
typedef char ElemType;

typedef struct node 
{     
    ElemType data;        /*数据域*/
    struct node *next;     /*指针域*/
} SLink;

双链表

1
2
3
4
5
6
7
typedef char ElemType;

typedef struct node
{    
    ElemType data;                /*数据域*/
    struct node *prior,*next;  /*分别指向前驱结点和后继结点的指针*/
} DLink;

3.顺序表的基本运算

3.1.线性表的定义

1
2
3
4
5
6
7
8
9
10
#include <stdio.h>
#define MAXSIZE 100 /*顺序表的容量*/

typedef char ElemType;

typedef struct
{
    ElemType data[MAXSIZE]; /*存放顺序表的元素*/
    int length;                /*顺序表的实际长度*/
} SqList;

3.2.初始化线性表

1
2
3
4
void InitList(SqList &sq) /*初始化线性表*/
{
    sq.length = 0;
}

3.3.求线性表长度

1
2
3
4
int GetLength(SqList sq) /*求线性表长度*/
{
    return sq.length;
}

3.4.求线性表中第i个元素

1
2
3
4
5
6
7
8
9
10
int GetElem(SqList sq, int i, ElemType &e) /*求线性表中第i个元素*/
{
    if (i < 1 || i > sq.length) /*无效的i值*/
        return 0;
    else
    {
        e = sq.data[i - 1];
        return 1;
    }
}

3.5.按值查找

1
2
3
4
5
6
7
8
9
10
int Locate(SqList sq, ElemType x) /*按值查找*/
{
    int i = 0;
    while (sq.data[i] != x) /*查找值为x的第1个结点*/
        i++;
    if (i > sq.length)
        return (0); /*未找到*/
    else
        return (i + 1);
}

3.6.插入元素

1
2
3
4
5
6
7
8
9
10
11
int InsElem(SqList &sq, ElemType x, int i) /*插入元素*/
{
    int j;
    if (i < 1 || i > sq.length + 1) /*无效的参数i*/
        return 0;
    for (j = sq.length; j > i; j--) /*将位置为i的结点及之后的结点后移*/
        sq.data[j] = sq.data[j - 1];
    sq.data[i - 1] = x; /*在位置i处放入x*/
    sq.length++;        /*线性表长度增1*/
    return 1;
}

3.7.删除元素

1
2
3
4
5
6
7
8
9
10
int DelElem(SqList &sq, int i) /*删除元素*/
{
    int j;
    if (i < 1 || i > sq.length) /*无效的参数i*/
        return 0;
    for (j = i; j < sq.length; j++) /*将位置为i的结点之后的结点前移*/
        sq.data[j - 1] = sq.data[j];
    sq.length--; /*线性表长度减1*/
    return 1;
}

3.8.输出线性表

1
2
3
4
5
6
7
void DispList(SqList sq) /*输出线性表*/
{
    int i;
    for (i = 1; i <= sq.length; i++)
        printf("%c ", sq.data[i - 1]);
    printf("\n");
}

3.9.main

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void main()
{
    int i;
    ElemType e;
    SqList sq;
    InitList(sq);         /*初始化顺序表sq*/
    InsElem(sq, 'a', 1); /*插入元素*/
    InsElem(sq, 'c', 2);
    InsElem(sq, 'a', 3);
    InsElem(sq, 'e', 4);
    InsElem(sq, 'd', 5);
    InsElem(sq, 'b', 6);
    printf("线性表:");
    DispList(sq);
    printf("长度:%d\n", GetLength(sq));
    i = 3;
    GetElem(sq, i, e);
    printf("第%d个元素:%c\n", i, e);
    e = 'a';
    printf("元素%c是第%d个元素\n", e, Locate(sq, e));
    i = 4;
    printf("删除第%d个元素\n", i);
    DelElem(sq, i);
    printf("线性表:");
    DispList(sq);
}

4.单链表的基本运算

4.1.单链表的定义

1
2
3
4
5
6
7
8
9
10
#include <stdio.h>
#include <malloc.h>

typedef char ElemType;

typedef struct node 
{     
    ElemType data;        /*数据域*/
    struct node *next;     /*指针域*/
} SLink;

4.2.初始化单链表

1
2
3
4
5
void InitList(SLink *&L)     /*L作为引用型参数*/
{
    L=(SLink *)malloc(sizeof(SLink));  /*创建头结点*L*/
    L->next=NULL;
}

4.3.求线性表的长度

1
2
3
4
5
6
7
8
9
10
11
int GetLength(SLink *L)    /*求线性表的长度*/
{
    int i=0;
    SLink *p=L->next;
    while (p!=NULL) 
    {
        i++;
        p=p->next;
    }
    return i;
}

4.4.求线性表中第i个元素

1
2
3
4
5
6
7
8
9
10
11
12
13
int GetElem(SLink *L,int i,ElemType &e)    /*求线性表中第i个元素*/
{
    int j=1;
    SLink *p=L->next;  
    if (i<1 || i>GetLength(L)) 
        return(0);                /*i参数不正确,返回0*/
    while (j<i)                  /*从第1个结点开始找,查找第i个结点*/
    { 
        p=p->next;j++;
    }
    e=p->data;
    return(1);                  /*返回1*/
}

4.5.按值查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int Locate(SLink *L,ElemType x)    /*按值查找*/
{
    int i=1;
    SLink *p=L->next;
    while (p!=NULL && p->data!=x)      /*从第1个结点开始查找data域为x的结点*/
    {
        p=p->next;
        i++;
    }
    if (p==NULL)
        return(0);
    else
        return(i);
}

4.6.插入结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int InsElem(SLink *L,ElemType x,int i)    /*插入结点*/
{
    int j=1;
    SLink *p=L,*s;
    s=(SLink *)malloc(sizeof(SLink));    /*创建data域为x的结点*/
    s->data=x;s->next=NULL;
    if (i<1 || i>GetLength(L)+1) 
    return 0;            /*i参数不正确,插入失败,返回0*/
    while (j<i)          /*从头结点开始找,查找第i-1个结点,由p指向它*/
    {  
        p=p->next;j++;
    }
    s->next=p->next;     /*将*s的next域指向*p的下一个结点(即第i个结点)*/
    p->next=s;            /*将*p的next域指向*s,这样*s变成第i个结点*/
    return 1;           /*插入运算成功,返回1*/
}

4.7.删除结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int DelElem(SLink *L,int i)    /*删除结点*/
{
    int j=1;
    SLink *p=L,*q;
    if (i<1 || i>GetLength(L)) 
        return 0;       /*i参数不正确,插入失败,返回0*/
    while (j<i)            /*从头结点开始,查找第i-1个结点,由p指向它*/
    {
        p=p->next;j++;
    }
    q=p->next;          /*由q指向第i个结点*/
    p->next=q->next;    /*将*p的next指向*q之后结点,即从链表中删除第i个结点*/
    free(q);                /*释放第i个结点占用的空间*/
    return 1;            /*删除运算成功,返回1*/
}

4.8.输出单链表

1
2
3
4
5
6
7
8
9
10
void DispList(SLink *L)    /*输出单链表*/
{
    SLink *p=L->next;
    while (p!=NULL) 
    {
        printf("%c ",p->data);
        p=p->next;
    }
    printf("\n");
}

4.9.main

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void main()
{
    int i;
    ElemType e;
    SLink *L;
    InitList(L);        /*初始化单链表L*/
    InsElem(L,'a',1);    /*插入元素*/
    InsElem(L,'c',2);
    InsElem(L,'a',3);
    InsElem(L,'e',4);
    InsElem(L,'d',5);
    InsElem(L,'b',6);
    printf("线性表:");DispList(L);
    printf("长度:%d\n",GetLength(L));
    i=3;GetElem(L,i,e);
    printf("第%d个元素:%c\n",i,e);
    e='a';
    printf("元素%c是第%d个元素\n",e,Locate(L,e));
    i=4;printf("删除第%d个元素\n",i);
    DelElem(L,i);
    printf("线性表:");DispList(L);
}

5.链表的基本运算(By-Go)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
// Package linkedlist creates a ItemLinkedList data structure for the Item type
package linkedlist

import (
    "fmt"
    "sync"
)

// Item the type of the linked list
type Item interface{}

// Node a single node that composes the list
type Node struct {
    content Item
    next    *Node
}

// ItemLinkedList the linked list of Items
type ItemLinkedList struct {
    head *Node
    size int
    lock sync.RWMutex
}

// Append adds an Item to the end of the linked list
func (ll *ItemLinkedList) Append(t Item) {
    ll.lock.Lock()
    node := Node{t, nil}
    if ll.head == nil {
        ll.head = &node
    } else {
        last := ll.head
        for {
            if last.next == nil {
                break
            }
            last = last.next
        }
        last.next = &node
    }
    ll.size++
    ll.lock.Unlock()
}

// Insert adds an Item at position i
func (ll *ItemLinkedList) Insert(i int, t Item) error {
    ll.lock.Lock()
    defer ll.lock.Unlock()
    if i < 0 || i > ll.size {
        return fmt.Errorf("Index out of bounds")
    }
    addNode := Node{t, nil}
    if i == 0 {
        addNode.next = ll.head
        ll.head = &addNode
        return nil
    }
    node := ll.head
    j := 0
    for j < i-2 {
        j++
        node = node.next
    }
    addNode.next = node.next
    node.next = &addNode
    ll.size++
    return nil
}

// RemoveAt removes a node at position i
func (ll *ItemLinkedList) RemoveAt(i int) (*Item, error) {
    ll.lock.Lock()
    defer ll.lock.Unlock()
    if i < 0 || i > ll.size {
        return nil, fmt.Errorf("Index out of bounds")
    }
    node := ll.head
    j := 0
    for j < i-1 {
        j++
        node = node.next
    }
    remove := node.next
    node.next = remove.next
    ll.size--
    return &remove.content, nil
}

// IndexOf returns the position of the Item t
func (ll *ItemLinkedList) IndexOf(t Item) int {
    ll.lock.RLock()
    defer ll.lock.RUnlock()
    node := ll.head
    j := 0
    for {
        if node.content == t {
            return j
        }
        if node.next == nil {
            return -1
        }
        node = node.next
        j++
    }
}

// IsEmpty returns true if the list is empty
func (ll *ItemLinkedList) IsEmpty() bool {
    ll.lock.RLock()
    defer ll.lock.RUnlock()
    if ll.head == nil {
        return true
    }
    return false
}

// Size returns the linked list size
func (ll *ItemLinkedList) Size() int {
    ll.lock.RLock()
    defer ll.lock.RUnlock()
    size := 1
    last := ll.head
    for {
        if last == nil || last.next == nil {
            break
        }
        last = last.next
        size++
    }
    return size
}

// Insert adds an Item at position i
func (ll *ItemLinkedList) String() {
    ll.lock.RLock()
    defer ll.lock.RUnlock()
    node := ll.head
    j := 0
    for {
        if node == nil {
            break
        }
        j++
        fmt.Print(node.content)
        fmt.Print(" ")
        node = node.next
    }
    fmt.Println()
}

// Head returns a pointer to the first node of the list
func (ll *ItemLinkedList) Head() *Node {
    ll.lock.RLock()
    defer ll.lock.RUnlock()
    return ll.head
}

6.循环单链表的基本运算

6.1.循环单链表的定义

1
2
3
4
5
6
7
8
9
10
#include <stdio.h>
#include <malloc.h>

typedef char ElemType;

typedef struct node 
{     
    ElemType data;            /*数据域*/
    struct node *next;         /*指针域*/
} SLink;

6.2.初始化循环单链表

1
2
3
4
5
void InitList(SLink *&L)       /*初始化线性表,L为引用型参数*/
{
    L=(SLink *)malloc(sizeof(SLink));
    L->next=L;
}

6.3.求线性表的长度

1
2
3
4
5
6
7
8
9
10
int GetLength(SLink *L)    /*求线性表的长度*/
{
    int i=0;
    SLink *p=L->next;
    while (p!=L) 
    {
        i++;p=p->next;
    }
    return i;
}

6.4.求线性表中第i个元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int GetElem(SLink *L,int i,ElemType &e)    /*求线性表中第i个元素*/
{
    int j=1;
    SLink *p=L->next;  
    if (i<1 || i>GetLength(L)) 
        return(0);            /*i参数不正确,返回0*/
    while (j<i)              /*从第1个结点开始,查找第i个结点*/
    {     
        p=p->next;
        j++;
    }
    e=p->data;
    return(1);              /*返回1*/
}

6.5.按值查找

1
2
3
4
5
6
7
8
9
10
11
12
13
int Locate(SLink *L,ElemType x)    /*按值查找*/
{
    int i=1;
    SLink *p=L->next;
    while (p!=L && p->data!=x)      /*从第1个结点开始查找data域为x的结点*/
    {    p=p->next;
        i++;
    }
    if (p==L)
        return(0);
    else
        return(i);
}

6.6.插入结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int InsElem(SLink *L,ElemType x,int i)    /*插入结点*/
{
    int j=1;
    SLink *p=L,*s;
    s=(SLink *)malloc(sizeof(SLink));
    s->data=x;s->next=NULL;
    if (i<1 || i>GetLength(L)+1) 
        return 0;
    while (j<i) 
    {
        p=p->next;j++;
    }
    s->next=p->next;
    p->next=s;
    return 1;
}

6.7.删除结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int DelElem(SLink *L,int i)    /*删除结点*/
{
    int j=1;
    SLink *p=L,*q;
    if (i<1 || i>GetLength(L)) 
        return 0;
    while (j<i) 
    {
        p=p->next;j++;
    }
    q=p->next;
    p->next=q->next;
    free(q);
    return 1;
}

6.8.输出线性表

1
2
3
4
5
6
7
8
9
void DispList(SLink *L)    /*输出线性表*/
{
    SLink *p=L->next;
    while (p!=L) 
    {
        printf("%c ",p->data);p=p->next;
    }
    printf("\n");
}

6.9.main

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void main()
{
    int i;
    ElemType e;
    SLink *L;
    InitList(L);        /*初始化单链表L*/
    InsElem(L,'a',1);    /*插入元素*/
    InsElem(L,'c',2);
    InsElem(L,'a',3);
    InsElem(L,'e',4);
    InsElem(L,'d',5);
    InsElem(L,'b',6);
    printf("线性表:");DispList(L);
    printf("长度:%d\n",GetLength(L));
    i=3;GetElem(L,i,e);
    printf("第%d个元素:%c\n",i,e);
    e='a';
    printf("元素%c是第%d个元素\n",e,Locate(L,e));
    i=4;printf("删除第%d个元素\n",i);
    DelElem(L,i);
    printf("线性表:");DispList(L);
}

7.双链表的基本运算

7.1.双链表的定义

1
2
3
4
5
6
7
8
9
10
#include <stdio.h>
#include <malloc.h>

typedef char ElemType;

typedef struct node
{    
    ElemType data;                /*数据域*/
    struct node *prior,*next;  /*分别指向前驱结点和后继结点的指针*/
} DLink;

7.2.初始化双链表

1
2
3
4
5
void InitList(DLink *&L)
{
    L=(DLink *)malloc(sizeof(DLink));  /*创建头结点*L*/
    L->prior=L->next=NULL;
}

7.3.求表长运算

1
2
3
4
5
6
7
8
9
10
int GetLength(DLink *L)    /*求表长运算*/
{
    int i=0;
    DLink *p=L->next;
    while (p!=NULL) 
    {
        i++;p=p->next;
    }
    return i;
}

7.4.求线性表中第i个元素

1
2
3
4
5
6
7
8
9
10
11
12
13
int GetElem(DLink *L,int i,ElemType &e)    /*求线性表中第i个元素*/
{
    int j=1;
    DLink *p=L->next;  
    if (i<1 || i>GetLength(L)) 
        return(0);                /*i参数不正确,返回0*/
    while (j<i)                  /*从第1个结点开始,查找第i个结点*/
    { 
        p=p->next;j++;
    }
    e=p->data;
    return(1);                  /*返回1*/
}

7.5.按值查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int Locate(DLink *L,ElemType x)    /*按值查找*/
{
    int i=1;
    DLink *p=L->next;
    while (p!=NULL && p->data!=x)      /*从第1个结点开始查找data域为x的结点*/
    {
        p=p->next;
        i++;
    }
    if (p==NULL)
        return(0);
    else
        return(i);
}

7.6.插入运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int InsElem(DLink *L,ElemType x,int i)    /*插入运算*/
{
    int j=1;
    DLink *p=L,*s;
    s=(DLink *)malloc(sizeof(DLink));      /*创建data域为x的结点*/
    s->data=x;s->prior=s->next=NULL;
    if (i<1 || i>GetLength(L)+1)        /*i参数不正确,插入失败,返回0*/
        return 0;
    while (j<i)              /*找到第i-1个结点,由p指向它*/
    {
            p=p->next;j++;
    }
    s->next=p->next;           /**s的next域指向*p的下一个结点*/
    s->prior=p;             /**s的prior域指向*p*/
    if (p->next!=NULL)      /*若*p不是最后结点,则将*p之后结点的prior域指向*s*/
        s->next->prior=s;
     p->next=s;              /**p的next域指向*s*/
    return 1;                 /*插入运算成功,返回1*/
}

7.7.删除运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int DelElem(DLink *L,int i)    /*删除运算*/
{
    int j=1;
    DLink *p=L,*q;
    if (i<1 || i>GetLength(L))    /*i参数不正确,删除失败,返回0*/
        return 0;
    while (j<i)                /*找到第i-1个结点,由p指向它*/
    {
           p=p->next;j++;
    }
    q=p->next;                 /*q指向*p的下一个结点,即要删除的结点*/
    p->next=q->next;
    if (q->next!=NULL)        /*若*q不是最后结点,则将*q之后结点的prior域指向*p*/
        q->next->prior=p;
    free(q);                    /*释放第i个结点占用的空间*/
    return 1;                   /*删除运算成功,返回1*/
}

7.8.输出线性表

1
2
3
4
5
6
7
8
9
void DispList(DLink *L)    /*输出线性表*/
{
    DLink *p=L->next;
    while (p!=NULL) 
    {
        printf("%c ",p->data);p=p->next;
    }
    printf("\n");
}

7.9.main

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void main()
{
    int i;
    ElemType e;
    DLink *L;
    InitList(L);        /*初始化双链表L*/
    InsElem(L,'a',1);    /*插入元素*/
    InsElem(L,'c',2);
    InsElem(L,'a',3);
    InsElem(L,'e',4);
    InsElem(L,'d',5);
    InsElem(L,'b',6);
    printf("线性表:");DispList(L);
    printf("长度:%d\n",GetLength(L));
    i=3;GetElem(L,i,e);
    printf("第%d个元素:%c\n",i,e);
    e='a';
    printf("元素%c是第%d个元素\n",e,Locate(L,e));
    i=4;printf("删除第%d个元素\n",i);
    DelElem(L,i);
    printf("线性表:");DispList(L);
}

8.循环双链表的基本运算

8.1.循环双链表的定义

1
2
3
4
5
6
7
8
9
10
#include <stdio.h>
#include <malloc.h>

typedef char ElemType;

typedef struct node
{    
    ElemType data;                /*数据域*/
    struct node *prior,*next;  /*分别指向前驱结点和后继结点的指针*/
} DLink;

8.2.初始化循环双链表

1
2
3
4
5
void InitList(DLink *&L)
{
    L=(DLink *)malloc(sizeof(DLink));
    L->prior=L->next=L;
}

8.3.求表长运算

1
2
3
4
5
6
7
8
9
10
int GetLength(DLink *L)    /*求表长运算*/
{
    int i=0;
    DLink *p=L->next;
    while (p!=L) 
    {
        i++;p=p->next;
    }
    return i;
}

8.4.求线性表中第i个元素

1
2
3
4
5
6
7
8
9
10
11
12
13
int GetElem(DLink *L,int i,ElemType &e)    /*求线性表中第i个元素*/
{
    int j=1;
    DLink *p=L->next;  
    if (i<1 || i>GetLength(L)) 
        return(0);                /*i参数不正确,返回0*/
    while (j<i)                  /*从第1个结点开始,查找第i个结点*/
    { 
        p=p->next;j++;
    }
    e=p->data;
    return(1);                  /*返回1*/
}

8.5.按值查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int Locate(DLink *L,ElemType x)    /*按值查找*/
{
    int i=1;
    DLink *p=L->next;
    while (p!=L && p->data!=x)      /*从第1个结点开始查找data域为x的结点*/
    {
        p=p->next;
        i++;
    }
    if (p==L)
        return(0);
    else
        return(i);
}

8.6.插入运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int InsElem(DLink *L,ElemType x,int i)    /*插入运算*/
{
    int j=1;
    DLink *p=L,*s;
    s=(DLink *)malloc(sizeof(DLink));
    s->data=x;s->prior=s->next=NULL;
    if (i<1 || i>GetLength(L)+1) 
            return 0;
    while (j<i)              /*找到第i-1个结点,由p指向它*/
    {
           p=p->next;j++;
    }
    s->next=p->next;      /*s的next域指向p之后的结点*/
    s->next->prior=s;     /*p之后结点的prior域指向s*/
    p->next=s;             /*p的next域指向s*/
    s->prior=p;            /*s的prior域指向p*/
    return 1;
}

8.7.删除运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int DelElem(DLink *L,int i)    /*删除运算*/
{
    int j=1;
    DLink *p=L,*q;
    if (i<1 || i>GetLength(L)) 
            return 0;
    while (j<i)         /*找到第i-1个结点,由p指向它*/
    {
           p=p->next;j++;
    }
    q=p->next;          /*q指向p的下一个结点,即要删除的结点*/
    p->next=q->next;       /*p的next指向q的下一个结点*/
    q->next->prior=p;    /*q的下一个结点的prior域指向p*/
    free(q);            /*释放q所占用的空间*/
    return 1;
}

8.8.输出线性表

1
2
3
4
5
6
7
8
9
void DispList(DLink *L)    /*输出线性表*/
{
    DLink *p=L->next;
    while (p!=L) 
    {
        printf("%c ",p->data);p=p->next;
    }
    printf("\n");
}

8.9.main

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void main()
{
    int i;
    ElemType e;
    DLink *L;
    InitList(L);        /*初始化双链表L*/
    InsElem(L,'a',1);    /*插入元素*/
    InsElem(L,'c',2);
    InsElem(L,'a',3);
    InsElem(L,'e',4);
    InsElem(L,'d',5);
    InsElem(L,'b',6);
    printf("线性表:");DispList(L);
    printf("长度:%d\n",GetLength(L));
    i=3;GetElem(L,i,e);
    printf("第%d个元素:%c\n",i,e);
    e='a';
    printf("元素%c是第%d个元素\n",e,Locate(L,e));
    i=4;printf("删除第%d个元素\n",i);
    DelElem(L,i);
    printf("线性表:");DispList(L);
}

9.顺序表求约瑟夫问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <stdio.h>
#define MaxSize 50

void jose(int n,int m)
{
    int mon[MaxSize];            /*存放n个猴子的编号*/
    int i,d,count;
    for (i=0;i<n;i++)            /*设置猴子的编号*/
        mon[i]=i+1;
    printf("出队前:");            /*输出出列前的编号*/
    for (i=0;i<n;i++) 
        printf("%d ",mon[i]);
    printf("\n");
    printf("出队后:");
    count=0;                    /*记录退出圈外的猴子个数*/
    i=-1;                        /*从0号位置的猴子开始计数*/
    while (count<n)
    {
        d=0;
        while (d<m)                /*累计m个猴子*/
        {
            i=(i+1)%n;
            if (mon[i]!=0)
                d++;
        }
        printf("%d ",mon[i]);    /*猴子出列*/
        mon[i]=0;
        count++;                /*出列数增1*/
    }
    printf("\n");
}

void main()
{
    int m,n;
    printf("输入猴子个数n,m:");
    scanf("%d%d",&n,&m);
    jose(n,m);
}

10.两个多项式相加运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
#include <stdio.h>
#include <malloc.h>

typedef struct node
{      float coef;            /*序数*/
       int expn;              /*指数*/
       struct node *next;    /*指向下一个结点的指针*/
} PolyNode;

void InitList(PolyNode *&L)        /*初始化多项式单链表*/
{
    L=(PolyNode *)malloc(sizeof(PolyNode));    /*建立头结点*/
    L->next=NULL;
}

int GetLength(PolyNode *L)        /*求多项式单链表的长度*/
{
    int i=0;
    PolyNode *p=L->next;
    while (p!=NULL)        /*扫描单链表L,用i累计数据结点个数*/
    {
        i++;p=p->next;
    }
    return i;
}

PolyNode *GetElem(PolyNode *L,int i)    /*返回多项式单链表中第i个结点的指针*/
{
    int j=1;
    PolyNode *p=L->next;
    if (i<1 || i>GetLength(L)) 
           return NULL;
    while (j<i)                /*沿next域找第i个结点*/
    {
           p=p->next;j++;
    }
    return p;
}

PolyNode *Locate(PolyNode *L,float c,int e)    /*在多项式单链表中按值查找*/
{
    PolyNode *p=L->next;
    while (p!=NULL && (p->coef!=c ||p->expn!=e))
            p=p->next;
    return p;
}

int InsElem(PolyNode *&L,float c,int e,int i)  /*在多项式单链表中插入一个结点*/
{
    int j=1;
    PolyNode *p=L,*s;
    s=(PolyNode *)malloc(sizeof(PolyNode));
    s->coef=c;s->expn=e;s->next=NULL;
    if (i<1 || i>GetLength(L)+1) 
        return 0;
    while (j<i)        /*查找第i-1个结点*p*/
    {
        p=p->next;j++;
    }
    s->next=p->next;
    p->next=s;
    return 1;
}

int DelElem(PolyNode *L,int i)        /*在多项式单链表中删除一个结点*/
{
    int j=1;
    PolyNode *p=L,*q;
    if (i<1 || i>GetLength(L)) 
        return 0;
    while (j<i)        /*在单链表中查找第i-1个结点*p*/
    {
        p=p->next;j++;
    }
    q=p->next;
    p->next=q->next;
    free(q);
    return 1;
}

void DispList(PolyNode *L)        /*输出多项式单链表的元素值*/
{
    PolyNode *p=L->next;
    while (p!=NULL)
    {
        printf("(%g,%d) ",p->coef,p->expn);
        p=p->next;
    }
    printf("\n");
}
void CreaPolyList(PolyNode *&L,float C[],int E[],int n)
{
    int i;
    InitList(L);
    for (i=0;i<n;i++)
        InsElem(L,C[i],E[i],i+1);
}

void SortPloy(PolyNode *&L)    /*对L的多项式单链表按expn域递增排序*/
{
    PolyNode *p=L->next,*q,*pre;
    L->next=NULL;
    while (p!=NULL) 
    {
        if (L->next==NULL)                     /*处理第1个结点*/
        {
            L->next=p;p=p->next;
            L->next->next=NULL;
           }
        else                                  /*处理其余结点*/
        {
            pre=L;q=pre->next;
            while (q!=NULL && p->expn>q->expn)     /*找q->expn刚大于或等于p->expn的结点*q的前驱结点*pre*/
            {
                pre=q;q=q->next;
            }
            q=p->next;                      /*在*pre结点之后插入*p*/
            p->next=pre->next;
            pre->next=p;
            p=q;
        }    
    }
}

PolyNode *AddPoly(PolyNode *pa,PolyNode *pb)
{
    PolyNode *pc,*p1=pa->next,*p2=pb->next,*p,*tc,*s;
    pc=(PolyNode *)malloc(sizeof(PolyNode));    /*新建头结点*/
    pc->next=NULL;                    /*pc为新建单链表的头结点*/
    tc=pc;                            /*tc始终指向新建单链表的最后结点*/
    while (p1!=NULL && p2!=NULL) 
    {
        if (p1->expn<p2->expn)        /*将*p1结点复制到*s并链到pc尾*/
        {
            s=(PolyNode *)malloc(sizeof(PolyNode));
            s->coef=p1->coef;s->expn=p1->expn;s->next=NULL;
            tc->next=s;tc=s;
            p1=p1->next;
        }
        else if (p1->expn>p2->expn)    /*将*p2结点复制到*s并链到pc尾*/
        {
            s=(PolyNode *)malloc(sizeof(PolyNode));
            s->coef=p2->coef;s->expn=p2->expn;s->next=NULL;
            tc->next=s;tc=s;
            p2=p2->next;
        }
        else   /*p1->expn=p2->expn的情况*/
        {
            if (p1->coef+p2->coef!=0) /*序数相加不为0时新建结点*s并链到pc尾*/
            {
                s=(PolyNode *)malloc(sizeof(PolyNode));
                s->coef=p1->coef+p2->coef;s->expn=p1->expn;
                s->next=NULL;
                tc->next=s;tc=s;
            }
            p1=p1->next;p2=p2->next;
        }
    }
    if (p1!=NULL) p=p1;  /*将尚未扫描完的余下结点复制并链接到pc单链表之后*/
    else p=p2;
    while (p!=NULL) 
    {
        s=(PolyNode *)malloc(sizeof(PolyNode));
        s->coef=p->coef;s->expn=p->expn;s->next=NULL;
        tc->next=s;tc=s;
        p=p->next;
    }
    tc->next=NULL;        /*新建单链表最后结点的next域置空*/
    return pc;
}

void main()
{
    PolyNode *L1,*L2,*L3;
    float C1[]={3,7,5,9},C2[]={-9,8,22};
    int E1[]={1,0,17,8},E2[]={8,1,7};
    InitList(L1);
    InitList(L2);
    InitList(L3);
    CreaPolyList(L1,C1,E1,4);
    CreaPolyList(L2,C2,E2,3);
    printf("两多项式相加运算\n");
    printf("     原多项式A:");DispList(L1);
    printf("     原多项式B:");DispList(L2);
    SortPloy(L1);
    SortPloy(L2);
    printf("排序后的多项式A:");DispList(L1);
    printf("排序后的多项式B:");DispList(L2);
    L3=AddPoly(L1,L2);
    printf("多项式相加结果:");DispList(L3);
}

栈

1.栈的基本概念

栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

1.1.栈的定义

栈是一种特殊的线性表，插入和删除操作在表的某一端进行，允许插入和删除操作的一端称为栈顶，另一端称为栈底。

可以把栈看作一个竖直的桶，每次只能放入一个元素，先放入的元素在下，后放入的元素在上，后放入的元素先出。

1.2.栈的特征

  • 后进先出（LIFO）

1.3.栈的基本运算

  • 初始化栈
  • 进栈
  • 出栈，即返回栈顶元素，并删除当前的栈顶元素
  • 取栈顶元素
  • 判断栈空

2.栈的存储结构

栈的结构定义主要包含以下属性：

  • data: 一维数组，用于保存栈中的元素
    • StackSize：栈的大小，即数组的大小
    • ElemType：元素的类型
  • top: 栈顶的指针

2.1.顺序存储结构

1
2
3
4
5
6
7
8
9
typedef char ElemType;

#define StackSize 100        /*顺序栈的初始分配空间*/

typedef struct 
{    
    ElemType data[StackSize];    /*保存栈中元素*/
    int top;                    /*栈指针*/
} SqStack;

2.2.链式存储结构

1
2
3
4
5
6
7
typedef char ElemType;

typedef struct lsnode 
{    
    ElemType data;            /*存储结点数据*/
    struct lsnode *next;    /*指针域*/
} LinkStack;

3.顺序栈基本运算

3.1.栈的定义

1
2
3
4
5
6
7
8
9
10
11
#include <stdio.h>

typedef char ElemType;

#define StackSize 100        /*顺序栈的初始分配空间*/

typedef struct 
{    
    ElemType data[StackSize];    /*保存栈中元素*/
    int top;                    /*栈指针*/
} SqStack;

3.2.初始化栈

1
2
3
4
void InitStack(SqStack &st)        /*st为引用型参数*/
{
    st.top=-1;
}

3.3.进栈运算

1
2
3
4
5
6
7
8
9
10
11
int Push(SqStack &st,ElemType x)    /*进栈运算,st为引用型参数*/
{
    if (st.top==StackSize-1)    /*栈满*/
        return 0;
    else                        /*栈不满*/
    {
        st.top++;
        st.data[st.top]=x;
        return 1;        
    }
}

3.4.出栈运算

1
2
3
4
5
6
7
8
9
10
11
int Pop(SqStack &st,ElemType &x)        /*出栈运算,st和x为引用型参数*/
{
    if (st.top==-1)        /*栈空*/
        return 0;
    else                /*栈不空*/
    {
        x=st.data[st.top];
        st.top--;
        return 1;
    }
}

3.5.取栈顶元素

1
2
3
4
5
6
7
8
9
10
int GetTop(SqStack st,ElemType &x)    /*取栈顶元素,x为引用型参数*/
{
    if (st.top==-1)        /*栈空*/
        return 0;
    else 
    {
        x=st.data[st.top];
        return 1;
    }
}

3.6.判断栈空运算

1
2
3
4
5
6
7
int StackEmpty(SqStack st)    /*判断栈空运算*/
{
    if (st.top==-1)    /*栈空*/
        return 1;
    else            /*栈不空*/
        return 0;
}

3.7.main

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void main()
{
    SqStack st;
    ElemType e;
    InitStack(st);
    printf("栈%s\n",(StackEmpty(st)==1?"空":"不空"));
    printf("a进栈\n");Push(st,'a');
    printf("b进栈\n");Push(st,'b');
    printf("c进栈\n");Push(st,'c');
    printf("d进栈\n");Push(st,'d');
    printf("栈%s\n",(StackEmpty(st)==1?"空":"不空"));
    GetTop(st,e);
    printf("栈顶元素:%c\n",e);
    printf("出栈次序:");
    while (!StackEmpty(st))
    {
        Pop(st,e);
        printf("%c ",e);
    }
    printf("\n");
}

4.链栈基本运算

4.1.链式栈的定义

1
2
3
4
5
6
7
8
9
#include <malloc.h>

typedef char ElemType;

typedef struct lsnode 
{    
    ElemType data;            /*存储结点数据*/
    struct lsnode *next;    /*指针域*/
} LinkStack;

4.2.初始化栈

1
2
3
4
void InitStack(LinkStack *&ls)        /*ls为引用型参数*/
{
    ls=NULL;
}

4.3.进栈运算

1
2
3
4
5
6
7
8
void Push(LinkStack *&ls,ElemType x)        /*进栈运算,ls为引用型参数*/
{
    LinkStack *p;
    p=(LinkStack *)malloc(sizeof(LinkStack));
    p->data=x;
    p->next=ls;
    ls=p;
}

4.4.出栈运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int Pop(LinkStack *&ls,ElemType &x)        /*出栈运算,ls为引用型参数*/
{
    LinkStack *p;
    if (ls==NULL)     /*栈空,下溢出*/
        return 0;
    else 
    {
        p=ls;
        x=p->data;
        ls=p->next;
        free(p);
           return 1;
    }
}

4.5.取栈顶元素运算

1
2
3
4
5
6
7
8
9
10
int GetTop(LinkStack *ls,ElemType &x)    /*取栈顶元素运算*/
{
    if (ls==NULL)     /*栈空,下溢出*/
        return 0;
    else 
    {
        x=ls->data;
           return 1;
       }
}

4.6.判断栈空运算

1
2
3
4
5
6
7
int StackEmpty(LinkStack *ls)    /*判断栈空运算*/
{
    if (ls==NULL)
        return 1;
    else
        return 0;
}

4.7.main

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void main()
{
    LinkStack *ls;
    ElemType e;
    InitStack(ls);
    printf("栈%s\n",(StackEmpty(ls)==1?"空":"不空"));
    printf("a进栈\n");Push(ls,'a');
    printf("b进栈\n");Push(ls,'b');
    printf("c进栈\n");Push(ls,'c');
    printf("d进栈\n");Push(ls,'d');
    printf("栈%s\n",(StackEmpty(ls)==1?"空":"不空"));
    GetTop(ls,e);
    printf("栈顶元素:%c\n",e);
    printf("出栈次序:");
    while (!StackEmpty(ls))
    {
        Pop(ls,e);
        printf("%c ",e);
    }
    printf("\n");
}

5.栈的基本运算(By-Go)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// Package stack creates a ItemStack data structure for the Item type
package stack

import (
    "sync"
)

// Item the type of the stack
type Item interface{}

// ItemStack the stack of Items
type ItemStack struct {
    items []Item
    lock  sync.RWMutex
}

// New creates a new ItemStack
func (s *ItemStack) New() *ItemStack {
    s.items = []Item{}
    return s
}

// Push adds an Item to the top of the stack
func (s *ItemStack) Push(t Item) {
    s.lock.Lock()
    s.items = append(s.items, t)
    s.lock.Unlock()
}

// Pop removes an Item from the top of the stack
func (s *ItemStack) Pop() *Item {
    s.lock.Lock()
    item := s.items[len(s.items)-1]
    s.items = s.items[0 : len(s.items)-1]
    s.lock.Unlock()
    return &item
}